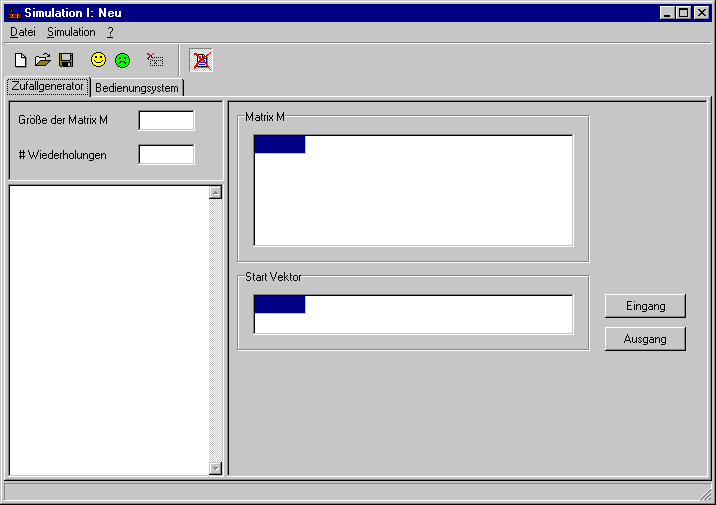
Das Programm ist selbsterklärend. Am untersten Rand werden
Erklärungen für das einzelne Button eingeblendet.Beispiele
Die Ergebnisse der einzelnen Auswertung (für verschiedene Phasentyp-Verteilungen) sind
hier ausgedruckt. Diese Datei sind auch in der Diskette gespeichert:
beispiel1.sim
Anzahl der Wiederholungen: 10000
Inhalt von Matrix M:
-4
Inhalt von Erweiterte Matrix:
-4 4
Inhalt von ÜbergangWS:
0 1
Inhalt von Startvektor:
1
--------------------------------------------------------
Erwartungswert = 0,228162316597388
Varianz = 0,00086822886825023
beispiel2.sim
Anzahl der Wiederholungen: 10000
Inhalt von Matrix M:
-3 3 0 0 0
0 -5 5 0 0
0 0 -1 1 0
0 0 0 -6 6
0 0 0 0 -2
Inhalt von Erweiterte Matrix:
-3 3 0 0 0 0
0 -5 5 0 0 0
0 0 -1 1 0 0
0 0 0 -6 6 0
0 0 0 0 -2 2
Inhalt von ÜbergangWS:
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
Inhalt von Startvektor:
1 0 0 0 0
--------------------------------------------------------
Erwartungswert = 2,00793988817093
Varianz = 0,0211925589026285
beispiel3.sim
Anzahl der Wiederholungen: 10000
Inhalt von Matrix M:
-3 0 0 0 0
0 -5 0 0 0
0 0 -1 0 0
0 0 0 -6 0
0 0 0 0 -2
Inhalt von Erweiterte Matrix:
-3 0 0 0 0 3
0 -5 0 0 0 5
0 0 -1 0 0 1
0 0 0 -6 0 6
0 0 0 0 -2 2
Inhalt von ÜbergangWS:
0 0 0 0 0 1
0 0 0 0 0 1
0 0 0 0 0 1
0 0 0 0 0 1
0 0 0 0 0 1
Inhalt von Startvektor:
0,2 0,3 0,1 0,15 0,25
--------------------------------------------------------
Erwartungswert = 0,340988656359623
Varianz = 0,0481515907188729
beispiel4.sim
Anzahl der Wiederholungen: 10000
Inhalt von Matrix M:
-2 1
2 -3
Inhalt von Erweiterte Matrix:
-2 1 1
2 -3 1
Inhalt von ÜbergangWS:
0 0,5 0,5
0,67 0 0,33
Inhalt von Startvektor:
0,5 0,5
--------------------------------------------------------
Erwartungswert = 0,920154410139871
Varianz = 0,457730718145889